Inverse Gamma Distribution PDF Calculator
For an Inverse Gamma distribution with shape parameter \(\alpha\) and scale parameter \(\beta\), the PDF is: $$ f(x;\alpha,\beta)=\frac{\beta^\alpha}{\Gamma(\alpha)}\,x^{-\alpha-1}e^{-\beta/x},\quad x>0. $$
* Enter \( x \) (with \( x>0 \)), \(\alpha>0\), and \(\beta>0\).
Step 1: Enter Parameters
Enter a value for \( x \) (must be \( > 0 \)).
e.g., 2
e.g., 3
Inverse Gamma Distribution Calculator
The Inverse Gamma distribution is a continuous probability distribution that is the reciprocal of the Gamma distribution. It is often used in Bayesian statistics, particularly as a conjugate prior for the precision parameter of a normal distribution.
Mathematically, the probability density function (PDF) of the Inverse Gamma distribution is defined as:
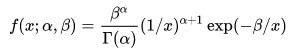
The Inverse Gamma distribution is characterized by its positive skewness and its support on the positive real numbers. It is often used to model variables that are bounded below by zero and have a right-skewed distribution of values.
Applications of the Inverse Gamma distribution include Bayesian estimation of scale parameters in regression models, Bayesian inference in hierarchical models, and modeling the uncertainty in variance components in s
Related Calculators
- Inverse Gamma Distribution Sample Generator: Generate random samples based on specified parameters (shape and scale).
- Inverse Gamma Distribution Mode Calculator: Compute the mode to identify the most frequently occurring value.
- Inverse Gamma Distribution Mean Calculator: Instantly calculate the mean (average) for α > 1.
- Inverse Gamma Distribution Inverse CDF Calculator: Calculate cumulative probabilities precisely at specific distribution points.
- Inverse Gamma Distribution PDF Calculator:
